Shasta Route speed zones
Part 1: South of Black Butte Junction
Curvature, possible speeds, and upgrade possibilities are very different along the Shasta Route. For good judgement, it is best to divide the route into speed zones. The following will be used:
- Southern Connections
- For Destinations south of Sacramento, data of the California high-speed rail project is used, with some corrections for the lower speed of Shasta Route trains. For other routes, the author will use the timings published for upgrade projects of the state of California.
- Zone 1: Sacramento to Red Bluff
-
There are two alternative routes north of Sacramento. The fastest one uses the former Western Pacific alignment between
Marysville (Binney Junction) and Sacramento (Hagen Junction). The current Amtrak "Coast Starlight" operation uses the former
Southern Pacific line via Roseville.
If Roseville station would be developed into a transit interconnection hub, there could be arguments in favour of the current Amtrak route, but the author assumes the fastest solution within this document. This reduces the geometrical speed restrictions between Sacramento and Red Bluff to just two points: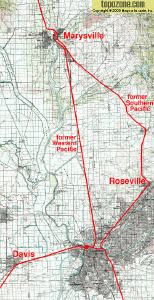
The two alignments between Sacramento and Marysville are best compared on a map.- Marysville with Binney Junction
- The Tehama bridge with its access curves
- Zone 2: Red Bluff to Milepost 233
- This part has minor restrictions by terrain, but for rather long parts. The tightest curve is No. 27 within the city of Red Bluff: 1848 feet radius.
- Zone 3: MP 233 to Redding
- This part is almost unrestricted, with the exception of the curve around Panorama Point (near Cottonwood). This is curve No. 41 with a radius of 2291 feet. It makes sense to slow down for this one curve.
- Zone 4: Circling Shasta Lake, Redding to Milepost 296
-
In 1942, the last train passed Shasta Dam on the old curvy alignment along the Sacramento River. The old railroad is located
under water since 1945, when work was completed on Shasta Lake, and the section of railroad track below the dam is used for
recreation today, called "Sacramento River Rail Trail".
The realignment faced difficult terrain, and is engineered as a freight route, not as a passenger track for high speed. Nonetheless, this part is considerably better engineered than the rest of the Sacramento River Canyon. Tightest curve is No. 86 at Pollock, 1348 feet radius. - Zone 5: The Sacramento River Canyon, MP 296 to Dunsmuir
-
The Sacramento runs in a narrow valley here, and the track winds along the river, giving an example of cheap engineering in
the 1880s. The typical curve has 574 feet radius, and the tightest one is No. 308, between the 12th Sacramento bridge and
Tunnel No. 15. Radius is 522 feet.
In this zone, there are only a few short stretches, that aren't speed-limited by the numerous 574 feet curves. - Zone 6: Sacramento River Canyon - the climb. Dunsmuir to Azalea (Mount Shasta)
- A legitimate part of Southern Pacific's "road of a thousand wonders", this part is great for sightseeing, less great for running trains. The former stations for railway tourism do not exist any longer. Curvature is the same as in Zone 5, but instead of few parts with potential for a higher speed limit, there are none. Tightest curve is No. 579 "Cantara Loop", with a radius of 410 feet.
- Zone 7: Azalea to Black Butte
- Black Butte is the junction with the traditional Shasta Route, the Siskiyou Line. The tightest curvature between Azalea and Black Butte is found at the northernmost end of the Mt. Shasta siding, curves No. 631 and 632 at 955 feet radius. This is an exception. Typical are curves of 1273 feet or more.
Politics and speed
Speed zones aren't created by geometry only, but also by politics. Upgrading a railroad has to look at certain "magic numbers", that make an upgrade more or less expensive. In the USA, the important magic numbers for passenger rail are 79 mph, 90 mph, 110 mph, and 125 mph. At these thresholds, costs for signaling or grade crossing protection change. This has a major influence on the total cost of an upgrade project.
Building a highspeed rail system, as planned in California, has a lot of positive effects. The usability is much better, in comparison to air service. It is convenient especially to those, who want to read or work during travel, attracting travelers of higher education. But the positive effects for connected areas create side effects for not-connected areas, as with any other transportation system.
If a French city does not have a TGV stop, or at least good connections to the system, it is very difficult to attract the headquarter of a major company, or important institutions of science or culture. The TGV system is one of the elements, that divide France into privileged locations and province. The economic importance of connection to highspeed rail has created European absurdities: Les Sables d'Olonne and the TGV Vendée were already mentioned in this document. In Germany, small towns have blackmailed the railway into provincial ICE stops, by blocking a highspeed line in the planning stage.
Local politicians in California, once having learned about the side effects of highspeed rail, will behave in similar ways as in Europe. This leads the author towards an assumption: After building the highspeed network, upgrade work in Northern California will be allowed to be one or two magic numbers more expensive, for political reasons, than before.
How this document will list track speed
Speeds and times will be calculated for the existing trackbed and curve radius, but the article will point to the most cost-effective possibilities for upgrades like curve straightening.